On this page we calculated a few things about objects that circle Earth. The fun part about physics is that you can often calculate things in completely different ways. Here we are going to calculate the velocity that for example a satellite in circular orbit has, taking an engineer's approach. This means that we'll use a few approximations rather than trying to calculate things exactly. Note that this stuff is inspired by an explanation by Richard Feynman. I can't recall the explanation exactly, so we'll start from scratch. Here it goes.

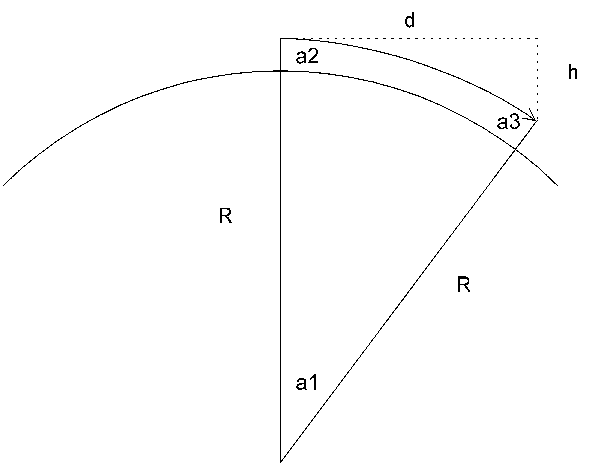
First it is important to realize that a satellite in orbit is actually falling. So, how come it doesn't crash into the Earth? Well, it has such a high velocity that it is actually falling around the Earth. Maybe the following picture will clarify things.

Our satellite is following the path indicated by the arrow. Now, let us for sake of simplicity consider the distance traveled in one second, since it makes things so much easier. In this one second our satellite "falls" the distance h, while traveling a horizontal distance d. The Earth's radius is indicated by R, and is approximately 6340 km, or 6340000 m.

We said we we would use approximations. The distance h is determined by h = 0.5 * a * t², which evaluates to 5 m, assuming that t = 1 second, and a = 10 m/s². So, our satellite will fall 5 meters in 1 second. Note that the scale of the picture above is grossly exaggerated for the numbers we are using.

Now, all we need to do is figure out what the value of d is, in meters. Since we assumed a time period of 1 second, we will then have our velocity in m/s.

We know that h is very small compared to R. So, we can essentially treat the figure as a triangle. This is where the angles a1, a2, and a3 come in. Some trigonometry now, you have to take it on faith...

sin( a1 ) / d = sin( a2 ) / (R + h) = sin ( a3 ) / R.

The only angle we know is a2, which is exactly 90 degrees or pi/2 radians . That means the sine of a2 is 1. Filling in the known values for R and h gives us:

sin( a1 ) / d = 1 / 6340005 = sin ( a3 ) / 6340000.

This results in sin( a3 ) = 6340000/6340005 = 0.999999211357088835103442347442944 (nothing like a bit of precision, huh?).

This allows us to calculate a3 as being equal to 1.56954042630932897263665706877753 radians (degrees are for carpenters). Since we know that the sum of angles in a triangle must be pi radians (or 180 degrees, if you're a carpenter), we can now determine that a1 = 0.00125590048556764659466462286221715 radians. Our distance d equals sin( a1 ) * R, or roughly 7962 meters, so our velocity is 7962 m/s, or 28664 km/h.

Which agrees nicely with known numbers. Note that we only needed the radius of the Earth and the acceleration of gravity to arrive at a result that is very close to the "known" value.

You can send me email at henkjan@oldeloohuis.com

Please send comments to webmaster@oldeloohuis.com.