Circular Orbits

Fun with rockets, satellites, and all that. How fast does a satellite need to go to stay in a circular orbit? And why are geostationary satellites at a fixed altitude?

Ok, first we make a few assumptions. We completely ignore relativity, that is, all these calculations strictly use Newton's laws. Furthermore, we assume we don't have to take air resistance into account (way too complicated).

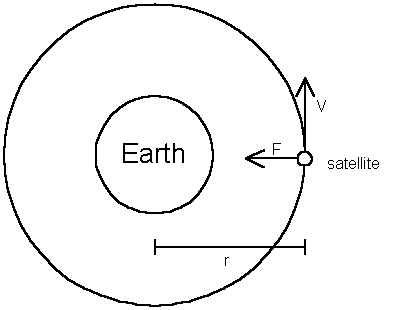
Let's take a satellite, for example, and let's assume it is circling Earth at an altitude of 130 km. Space is only a short drive away, if your car will go straight up. Look at the following picture (not to scale).

Our satellite is trying to get away from Earth, since it has a certain velocity v. However, Earth is pulling on the satellite (through gravity) with a force F, keeping it in a circular orbit (hopefully). The distance from the satellite to the center of the Earth is designated by r.

Note that this whole thing relies on tha fact that the gravitational mass of an object is identical to its inertial mass. As far as science knows, this is correct. But that's another story.

Ok, some cheating here. I am going to state a result for simplicity's sake, and that is the expression for the centripetal force required to make an object go in circles. You can google it if you don't believe me.

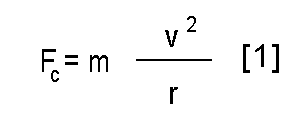
Where m is the mass of our satellite. The role of the centripetal force is played by gravitation. Thanks to Mr. Newton, it has been known for a long time that

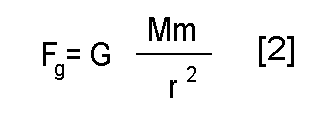
where G is the gravitational constant, and M is the mass of the Earth. Since the two expressions must be equal, we find that

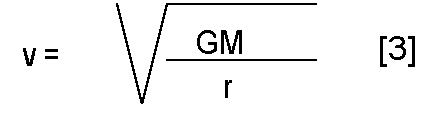
Since we know that r equals the radius of the Earth plus the altitude of the satellite (6370 km + 130 km = 6500 km), and

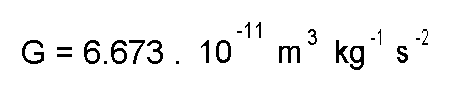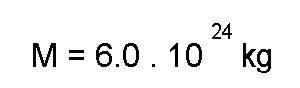
we find that

v = 7.848 km/s , which is a little more than 28,000 km/h, which agrees nicely with known results.

Ok, fine, on to the next problem, our geostationary satellite. In the previous example we chose the altitude of the satellite, and found a velocity from that. In the case of the geostationary satellite, we do not know the altitude, nor do we know the velocity. That seems like a bit of a problem. There is one thing we do know, however, and that is the satellite's angular velocity. Since the satellite has to be geostationary, that is, remain above the same location on Earth, we know that the satellite must orbit the Earth once every 24 hours.

Geostationary satellites must be over the equator. I'm not going to prove this here, try to figure out why. It might help to ask the question if you could have a stationary satellite over the North Pole.

We have the following relation between linear velocity, angular velocity, and radius.

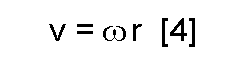
where is the angular velocity in radians per second. Since we know that the satellite must complete one orbit per 24 hours (86400 seconds), we find that

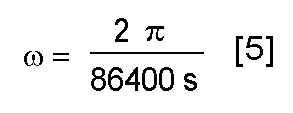
which equals 7.2722 * 10 ^-5 rad/s.

Using [4], we can write [1] in a different form

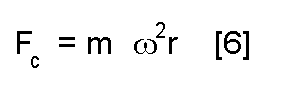
This must be equal to [2] again, so we can find the following expression for r

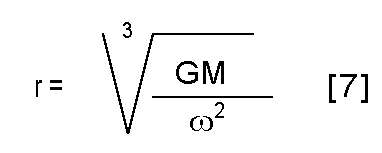
Filling in all known values, we find that r = 4.2304 * 10 ⁷ m = 42304 km.

So, subtracting the radius of the Earth (6370 km), we find that the altitude of a geostationary satellite must be approximately 35934 km. Any higher, and the satellite cannot keep up with the Earth while maintaining a circular orbit. Any lower, and it will rotate faster than Earth.

Please send comments to webmaster@oldeloohuis.com.