Nuclear Fusion

Time to talk physics again. This time about nuclear fusion, and some things that are not always immediately obvious.

An introduction. Ordinary matter contains of three different kind of particles. There's a whole zoo of exotic particles that play a role in nuclear physics, but they typically do not make up ordinary matter, so I'm going to ignore those buggers.

First, we have the proton. It is one of the two kinds of particles that make up an atomic nucleus. The proton has a positive electric charge.

Then there's the neutron. It's the other particle in the nucleus. It is just about as heavy as the proton (a teensy bit heavier) and it has no electric charge.

Third, we have the electron. It is quite a bit lighter than the proton and the neutron, and it has a negative electric charge. As a matter of fact, the charge of the electron is just as large as the charge of the proton, but it is negative rather than positive. Isn't that convenient?

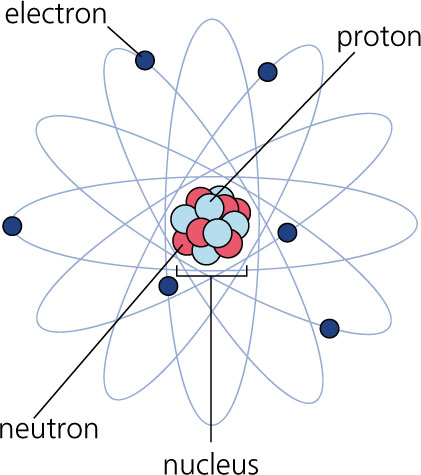
Atoms consist of a nucleus composed of protons and neutrons, and a bunch of electrons. According to the Bohr model of the atom, the electrons are circling the nucleus, much like planets orbit the sun. Like in the following picture, sort of.

Unfortunately, the Bohr model is incorrect. Quantum physics has something else to say about the atomic model. But quantum physics is bloody difficult. And the Bohr model is far easier to understand than quantum physics, and for this discussion it is more than adequate.

Typically, an atom has the same number of protons in the nucleus as electrons orbiting the nucleus, so the electric charges cancel each other out, so the whole is electrically neutral. Nice.

We're in trouble already, of course. Particles with the same electrical charge repel each other, and particles with an opposite electric charge attract each other. This poses two problems. First, why doesn't the atomic nucleus fall to pieces? The protons in the nucleus all have a positive charge, so they should repel each other. Enter the strong nuclear force. This is a sort of sub-atomic glue. As long as protons and neutrons (the glue works for neutrons too) are close enough together, the strong nuclear force makes them stick together. Sort of like glue.

As it happens, the strong nuclear force is much stronger than the electromagnetic force, so the glue wins, so to speak. Guess that's why they call it the strong nuclear force.

The second problem is trickier. Why don't the electrons crash into the nucleus? Particles with opposite charge attract each other, right? One explanation could be that they are circling the nucleus, and their velocity keeps them from falling down, much like the planets don't crash into the sun. Let's leave it at that. It is not accurate, unfortunately. The problem is that a thorough analysis requires quantum physics again. Let's just say that there's a problem with the explanation, but that quantum physics solves that problem, by postulating something truly bizarre. Then again, everything in quantum physics is bizarre.

Anyway, on to nuclear fusion. In school I learned that nuclear fusion, as it happens in the sun, involves taking four hydrogen nuclei (also known as protons, since the hydrogen atom consists of one proton and one electron, so the proton is the nucleus), and smashing them together rather violently, and producing a helium nucleus. All this produces a hell of a lot of energy. That's why the sun is so hot. There are actually more fusion reactions going on in stars, but let's keep it simple.

I also learned that you need very high temperatures and pressures to achieve this nuclear fusion stuff. This is rather logical, if we consider the following.

The electromagnetic force wants to keep the protons away from each other. The strong nuclear force wants to glue them together. Problem is that the strong nuclear force only works at very short distances, in other words, only when the protons are almost "touching" each other. Just like glue. However, the electromagnetic force also works at long distances (up to infinity, as a matter of fact). Granted, the strength of the electromagnetic force diminishes with distance, but still. So, the trick with nuclear fusion is to get the hydrogen nuclei (protons) so close together that the strong nuclear force can overcome the repelling electromagnetic force. There are two ways of doing this. The first is a high temperature. High temperature means that particles (the protons) are moving at high velocities. So, if two protons move at very high velocities toward each other, they may get close enough for the strong nuclear force to take over, and fuse them together. The other way is to have a high pressure. High pressure means that a lot of particles are close together, so there is more chance that they will be close enough for fusion to take place.

Summarizing, you need a high temperature and a high pressure to get nuclear fusion. Sort of like inside the sun.

This whole description is a bit simplistic, of course. The way that the sun (and other stars) achieved the right conditions to start fusion ('ignite') has to do with gravity. It's kinda complicated. Let's leave it at that.

Now for a more practical matter. How do we achieve nuclear fusion on Earth?

Well, in thermonuclear weapons (hydrogen bombs) it is kind of easy. You just detonate a "normal" nuclear weapon (a fission bomb) to get things hot and dense. Hydrogen bombs are kind of useless and dangerous, though. You would like to have a controlled fusion reaction so you can generate electricity rather than evaporate people.

Now I have to go back to atomic theory again. The simple form of hydrogen (one proton plus one electron ) isn't the only player on the block. There is also something called deuterium. This is hydrogen with a different nucleus: a proton and a neutron rather than just one proton.

So, why is deuterium still a form of hydrogen? Because it still only has one electron, that's why. The elements are classified in a chemical sense. The chemical reactions that atoms can participate in are determined by their electron configuration. The composition of the nucleus has no influence on chemical reactions. Deuterium has only one electron because the nucleus has only one proton. The electrical charges still cancel out. Neat.

Another aside: when deuterium binds with oxygen, it results in something called heavy water. The word heavy comes from the fact that a deuterium nucleus is heavier than a hydrogen nucleus. A little more than twice as heavy.

So, why is deuterium interesting for nuclear fusion? Well, it is much easier to smash a bunch of deuterium nuclei (or deuterons) together than it is for regular hydrogen. This is because the extra neutron in deuterium does not have any effect on the electromagnetic repulsion. A neutron does not have an electrical charge, remember? However, the extra neutron does have an effect on the strong nuclear force, since this force acts on protons and neutrons alike. Simply put, because of the extra neutron, it is easier to "glue" the nuclei together, and nuclear fusion becomes easier to achieve.

Interestingly enough, you can scoop deuterium out of the ocean. A certain percentage (0.015%) of the hydrogen in sea water is actually deuterium. Even better, it seems that the deuterium gets replenished automatically when you take it out of sea water. Pretty cool.

So, why not stick another neutron on the deuterium nucleus to make fusion even easier? As a matter of fact, such a form of hydrogen actually exists, and it is called tritium. Tritium consists of two neutrons, one proton, and one electron. It is rather unstable, though, in the sense that it falls apart (by itself) in a relatively short time. So, tritium actually has to be produced (in nuclear reactors) in practice.

Long story short: in order to achieve controlled nuclear fusion in a reactor, research is mostly focused on the so-called D-T reaction. You take a deuterium nucleus and a tritium nucleus, and you smash them together. One proton plus one neutron smashed together with one proton plus two neutrons results in two protons and three neutrons.

Gonna have to show this a little differently.

²H + ³H -> ⁴He (3.5 MeV) + n (14.1 MeV)

That's just physics mumbo-jumbo. In English: we smack one deuterium (²H) and one tritium (³H) nucleus together, and we end up with one helium nucleus (⁴He) which carries an amount of energy equal to 3.5 MeV (see below), plus a neutron (n) which carries an amount of energy equal to 14.1 MeV.

Stupid energy units. One MeV actually means one Mega electronVolt. Mega just means "million". So that would be 1,000,000 electronVolt. So what's an electronVolt? That's the charge of an electron (1.6 * 10^-19 Coulomb) multiplied by one Volt. Which boils down to 1.6 * 10^-19 Joules. Sigh. These MeV units are just more convenient than Joules for particle physics geeks.

There is another thing that we might want to check. Typically, the masses on both sides of the arrow needs to match. In simple terms, the mass before and after the reaction needs to be the same (well, not quite, but hopefully everything will become clear).

So, let's try to find out what the masses of all these things are. Funnily enough, physicists don't quite agree on these, but for our purposes the values should be accurate enough.

First, we introduce the unit of atomic mass, or u. This thing is defined as 1/12th of the mass of a carbon-12 atom. Yadayada, whatever. One u roughly equals 1.66053886 x 10^-27 kg. Ok.

A deuterium atom (²H) has a mass of something like 2.01355321270 u.
A tritium atom (³H) has a mass of something like 3.0160492 u.
So, the left side (²H + ³H) has a mass of 5.0296024127 u.

A helium atom (⁴He) has a mass of something like 4.002602 u.
A neutron (n) has a mass of something like 1.0086485 u.
So, the right side (⁴He + n) has a mass of 5.0112505 u.

Uh-oh. There is a difference of 0.0183519127 u. Doesn't seem like a lot, but where did it go?
Well, the missing mass was transformed into energy. Contrary to what was believed for centuries, mass is not conserved in reactions, whether nuclear or chemical. Energy is not conserved either. However, the combination of mass and energy is conserved.

Enter Al Einstein and his famous formula E = mc². This gives us the ratio of mass and energy, namely the speed of light (in vacuum) squared. Since c = 299,792,458 m/s, we know that c² = 89,875,517,873,681,764 m²/s². In a more manageable notation: 8.9875517873681764 x 10¹⁶ m²/s².

So, our missing mass (0.0183519127 u = 0.030474064193677522 x 10^-27 kg) corresponds to an energy of 0.024496124297677522 x 10^-27 kg * 8.9875517873681764 x 10¹⁶ m²/s² = 2.73887230112259 x 10^-12 Joules (J).
Converting this to electronVolts, we find that our missing mass corresponds to 17.1 MeV. The energy on the right side equals 14.1 + 3.5 = 17.6 MeV. Close enough.

Ok, back to our fusion reaction.

If you want helium as the end product, you have one spare neutron now. A helium nucleus consists of two protons and two neutrons. The spare neutron flies off (causing problems, but that's another issue), so we have a neat mechanism after all. Right?

Well, yes, but... oops.

What is happening inside the sun??? Well, supposedly:

4 ¹H -> ⁴He + energy.

However, how can four hydrogen nuclei make up a helium nucleus? In other words, can two of the four protons turn into neutrons???

Yes, they can. They don't tell you this in school, but there is a reaction called the proton-proton chain. It essentially turns two protons into a proton and a neutron (by transforming one of the protons into a neutron, through the weak nuclear force). To be more precise, the proton-proton chain turns two protons into a deuterium nucleus, but anyway. This also produces a positron (a positively charged electron) and a neutrino (an elusive bugger). The positron keeps the electrical charge in balance, the neutrino is needed to keep other forms of physical bookkeeping in balance. This is getting way too complex.

Anyway, the point is that nuclear fusion inside the sun involves quite a bit more that just fusing hydrogen into helium. The proton-proton chain is an extremely slow reaction, in other words, it happens only occasionally. That is actually a good thing. If the transformation of a proton into a neutron (and a positron and a neutrino) wasn't so difficult, the sun would have stopped shining a long time ago.
There are a few more reactions required to turn four protons into a helium nucleus, but I'll leave it at that. For now.

Another entry in the not-so-obvious category.

Please send comments to webmaster@oldeloohuis.com.