What is mass?
The more you learn about physics, the more confusing it gets.
What is mass? Should be easy enough, right? Turns out that it's not that simple.
Classical Physics
There are two kinds of mass: gravitational mass and inertial mass.
Gravitational mass is the mass in Newton's Law of Universal Gravitation.
![]()
There. basically this formula describes the (attractive) force between two bodies of mass m1 and m2, at a distance r (between the centers of the masses). There's a funky constant (G) in there as well. The m1 and m2 are gravitational masses.
Why do you care? Well, this law of gravitation thing keeps your feet on the ground. You see, one of the masses often represents the mass of the earth. And the earth has quite a bit of mass, roughly 6.0 x 1024 kg. That's a 6 followed by 24 zeros. The other mass often represents your own mass (not weight). The result is that the earth attracts you (and you attract the earth).
OK. Now for the other type of mass: inertial mass. This is the mass in another one of Newton's laws (Newton was a rather bright guy):
![]()
More precisely, that should be written as F = dp/dt = d(mv)/dt = vdm/dt + mdv/dt. Since dm/dt is 0 is most practical scenarios, the equation reduces to F = ma with a being dv/dt of course.
The formula describes the relationship between a force (F) applied to an object with a certain mass (m), and the acceleration (a) that is a result of this.
Inertia can be described informally as resistance against acceleration (sometimes described as resistance against motion, but that's just plain wrong). The more mass an object has the harder you have to push it to give it a certain acceleration. It's easier to throw a golf ball than it is to throw a basketball. Note that this is not because the basketball has a greater weight, it is because the basketball has a greater mass. All this applies in the International Space Station (where stuff is weightless) as well as on earth. Although (at least on earth) mass and weight are intimately connected, they are fundamentally two very different things.
This whole thing about weight is a can of worms which I shall leave closed for now...
If you paid attention, you probably noticed that this force thingy (F) appeared in both of the previous formulas. Let's manipulate them a little, and define the following:
m1 = ME = the mass of the
earth
m = m2 = the mass of a person being attracted by the earth's gravity.
So, then we get:
![]()
Now, if we equate the two expressions for F to find a person's acceleration (while jumping down, for example) due to gravity, we get:
![]() or
or
![]()
So, what is so interesting about this? Well, the acceleration of an object due to the earth's gravity is independent of the objects mass! Every object is accelerated the same, heavy or light.
Everyday experience seems to contradict this. A feather doesn't fall nearly as fast as a brick. That's because the atmosphere (air) messes things up here. On the moon (which has no atmosphere worth mentioning) a feather and brick do fall at the same speed.
Galileo (another bright man) was one of the first, if not the very first, to realize this. In his days people were convinced that heavier objects fall faster than light objects. Galileo's argument against this went something like this: say I have a metal ball that weighs 1 kilogram. A ball that weighs 2 kilograms is supposed to fall twice as fast. Now, what if I take two balls of 1 kilogram and connect them with a piece of string? Will the balls fall twice as fast just because they are now connected with a piece of string?
If you paid very close attention you may have noticed that we did something that is somewhat questionable in order to get to our formula for a. We deleted m from both sides of the equation. But on the left side, m represented inertial mass and on the right side it represented gravitational mass! What we did is only allowed if the two are identical (and not zero, but that's splitting hairs).
In other words: is inertial mass the same as gravitational mass?
As far as science knows, the answer to that is: yes.
Just for fun let's calculate the acceleration a due to the earth's gravity, usually indicated with "g". This is a simple matter of substituting:
G = 6.67 x 10-11 m3 kg-1 s-2 , ME = 5.97 x 1024 kg, r = 6.37x 106 m, and we find for g ( = a): 9.8134 ms-2
The official value (apparently) is : 9.8067 ms-2. Close enough.
I'm an engineer. One of the things you need to learn as an engineer is to decide when things are "good enough".
Relativity
Leave it to Al Einstein to complicate things.
Let's look at the most famous equation in the history of physics.
![]()
This equation relates the energy (E) of an object to it's mass (m), where c is the speed of light in a vacuum.
That c indicates the speed of light in a vacuum is rather important, since light waves propagate at different speeds in different media. The speed of light in vacuum is the universal speed limit. Nothing can go faster. As far as we know.
Einstein's famous equation is part of the theory of relativity. Note that there are two theories of relativity, the special theory of relativity and the general theory of relativity. While mere mortals at least have some chance of comprehending special relativity, general relativity requires a degree in higher mathematics before you can even start to try to figure it out.
Anyhow, I always interpreted E = mc2 as a formula to calculate the relationship between mass and energy when mass is converted to energy and energy is converted to mass. I always considered mass as a "frozen" form of energy, so to speak. I'll get back to that later on.
Nuclear Physics
Not that I know much about nuclear physics, but anyway.
An atom's nucleus consists of nucleons. A nucleon can either be a proton, which has a positive electric charge, or a neutron, which has no electric charge. Nucleons are made up of (three) quarks. There's also gluons that keep the quarks together. Gluons have no mass as far as scientists know, so we are ignoring them for now.
A proton is made up of two up quarks and one down quark. A neutron is made up of two down quarks and one up quark.
Quarks actually do have mass. For example, an up quark weighs about 1.5 - 4.0 MeV/c2
Whoa. Let's explain this a little. Particle physicists prefer to express masses of particles in electron Volts (eV). An electron Volt is nothing other than the charge of an electron multiplied by one Volt. This gives a result that has the physical dimension of energy (Joules). Energy and mass are related by E = mc2, so it the correct way is to say that mass has a physical dimension of eV/c2, but I guess that's just too cumbersome, since physicists typically express masses in eV. The electron Volt is a bit of an impractical unit, so particle masses are typically expressed as MeV (millions of electron Volts) or GeV (billions of electron Volts).
Then, a down quark weighs about 3.5 - 6.0 MeV/c2
Note that these masses are not very well known at all. Fortunately, that doesn't matter for the point I'm going to make.
If we add up the quark masses for a proton, we get a range of 6.5 - 14.0 MeV.
If we look up the (rather well known) mass of a proton, we find that it is 938.272 MeV/c2
Errr, that doesn't add up at all, now does it? A proton is between 67 times and 144 times heavier than the sum of its parts.
Where does the difference come from?
Binding energy. The ("strong") nuclear force that binds the quarks together into a proton is rather strong. Guess that's why it's called the strong force. Strong forces result in high (binding) energies.
So, the vast majority of the mass in a proton (or neutron for that matter) is actually energy.
So, my earlier assumption that mass and energy can be converted into each other is at least half inaccurate. "Energy can be converted into mass" No! Energy is mass! Both gravitational and inertial mass as a matter of fact, since the two are identical.
So, does the opposite: "mass is energy" hold true? Short answer: don't know.
All the above was inspired by the fact that I was reading a book (called The Lightness of Being) about physics, matter and the like. The writer is a man named Frank Wilczek, and he must know what he is talking about since they gave him the Nobel Prize for physics in 2004.
I have a problem with books about physics. They are either too much aimed at the general public, and as a consequence hardly contain any equations, since conventional wisdom states that every equation halves the sale of a popular physics book. Or, they are textbooks aimed at university physics students, and they make your head spin after two pages. You have to spend six months brushing up on your math just to be able to read them. There seems to be no middle ground. One notable exception is Relativity by Einstein himself. If I read that one four more times maybe I'll understand a little of it.
One thing is for certain: mass can be converted into energy, the process obeying E = mc2. Enter the bizarre world of antimatter. This stuff is not just a brain child of the writers of Star Trek, antimatter (or at least antiparticles) is (are) very real.
Take for example the antiparticle of the electron, the positron. This is a particle that is identical to an electron, but with an opposite electrical charge: the positron has a positive electrical charge. If you bring an electron and a positron together close enough, they annihilate: poof, gone, both of them. All that's left is pure energy, and yes, the relationship between the combined masses and the produced energy does indeed obey E = mc2
So, could the produced energy be binding energy, just like in the case of the proton discussed earlier? The answer is: unlikely. The established opinion in particle physics is that an electron is not built up of sub-particles like the nucleons are. Also, the quarks discussed earlier do have some mass "of their own", the mass of a nucleon is not totally made up of energy. There is no reason to suspect that quarks can be split.
Wilczek's book addresses the same question in a way. The answer to "what is mass" is basically: "well, in the case of nucleons it's mostly energy, and as far as the quark and electron masses are concerned, we don't know".
Relativistic Mass
I'm gong to go crazy now and put one of my own conclusions here. It may be totally wrong.
If you read about relativity, one thing you'll find out that, as mentioned earlier, there is an absolute speed limit in the universe and that is the speed of light in vacuum (c). This fact is one of the main postulates of the theory (theories) of relativity. Apparently it was necessary to assume this, since Maxwell's laws of electromagnetism would not make any sense at all without it. Don't ask me why.
One of the results of relativity is that the mass of an object increases as its velocity increases. This is called the relativistic mass. The relationship between relativistic mass (mr) and rest mass (m0) is as follows.
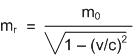
Where v is the velocity of the object, and c is the light speed in vacuum.
Smarter guys than me have figured this out, so why question it?
Anyway, that relationship neatly enforces the universal speed limit: as an object's velocity approaches the speed of light, it's relativistic mass becomes larger, hence it is harder to accelerate the object even more. For v = c, the relativistic mass is infinite, so that cannot happen.
Great. Now consider a particle in a particle accelerator. These things typically travel at more than 99% of the speed of light. If we put more energy in them (with magnetic fields) in order to accelerate them even more, where does the energy go?
Well, in the classical, non-relativistic case, the kinetic energy of an object (or particle) is given by Ek = 0.5 x mv2
So, if we apply a force to an object, we increase its velocity, thus increasing its kinetic energy. Back to the particle that is already at 99% of the speed of light. We cannot increase its speed much more, since the particle is already very close to the universal speed limit. So, where does the energy go that we add to it? Well, the only way is to increase its mass! As per the equation above.
Then again, I cannot help but wonder if I am confusing cause and effect here. Like I said, it may be totally wrtong. Must think more about it...
Please send comments to webmaster@oldeloohuis.com.