| Fun with Mathematics |
Fun with mathematics? Would it be possible? I happen to think so...
| Prime Numbers |
First an introduction. Prime numbers are defined as positive whole numbers that have exactly two (different) divisors. Examples: 2, 3, 5, 7, 11, 13,... Sometimes prime numbers are defined as positive whole numbers that can only be divided by 1 and by the number itself. All the examples listed before satisfy this definition. However there is one exception: 1. This number can be divided by 1 and by itself (1), therefore it would be a prime number according to the second definition. The number 1 is not considered to be a prime number, since it would cause a whole heap of problems with higher mathematics. Just take it on faith...
Anyway, there's a whole lot of fun to be had with prime numbers (or primes), but here we're going to prove the fact that there are infinitely many primes.
To prove this, we are going to assume that there are a limited number of primes, and then show that that leads to a contradiction. Therefore the opposite (there are infinitely many primes) must be true.
First, we need to recognize the fact that all non-primes are a product of primes. Just an example: take 20. It is not a prime, since we can divide it by 2. The result of the division is 10. We can divide 10 by 2. Result is 5, which is a prime. So, 20 = 2*2*5. The factors are all primes. But, we can also write: 20 = 4*5. And 4 is not a prime. But, we can factor 4 as 2*2, which leads us to the first result. So, the conclusion is: all non-primes can be written as a product of primes. If there is a factor that is not a prime, then we can factor this number into primes again. The consequence of this is: if we want to check if a number is a prime or not, we do not need to check all numbers to see if it is divisible, we only need to check all the primes (that are smaller than the number). Actually, we only need to check all prime numbers smaller than the square root of the candidate, but that doesn't really matter here.
So, let's go back and assume that there are a limited number of primes. Let's write them in order as: p1, p2, p3,...,pN, where pN is the highest prime. Now, lets construct a number called q, which is defined as (p1*p2*p3*...*pN)+1. So, in English, the product of all primes, plus 1. This number has to be a prime. You can't divide it by p1, since the remainder is 1. You can't divide it by p2, since the remainder is 1, etcetera. So, there is no highest prime number, since we can construct a higher one from all other primes.
More concrete: let's assume 2, 3, and 5 are the only primes, therefore 5 being the highest. We construct q as (2*3*5)+1 = 31. This is a prime (check it). So, there is no highest prime. So, there is an infinite number of primes. No matter how many you have found, you can always find a new one.
Note that this method just gives you a new prime, it does not give you all primes. The numbers 7, 11, 13, 17, 19, 23, and 29 are also prime, and they are smaller than 31.
| Triangles |
The sum of all angles in a triangle is 180°. At least that's what I learned in school. We can actually prove this.
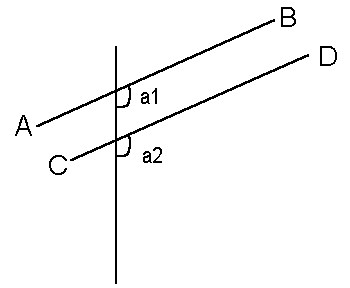
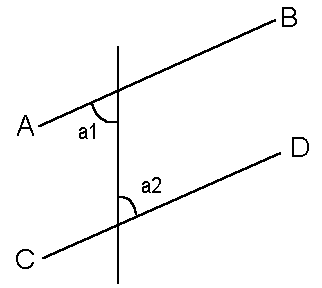
First consider the following pictures.


In both pictures, lines AB and CD are parallel. Take it on faith that this means that angles a1 and a2 are the same, in both pictures. The equality of the angles in the second picture actually follows from the first one. Never mind that.
Now, look at the following picture of a triangle, to which I have added another line.
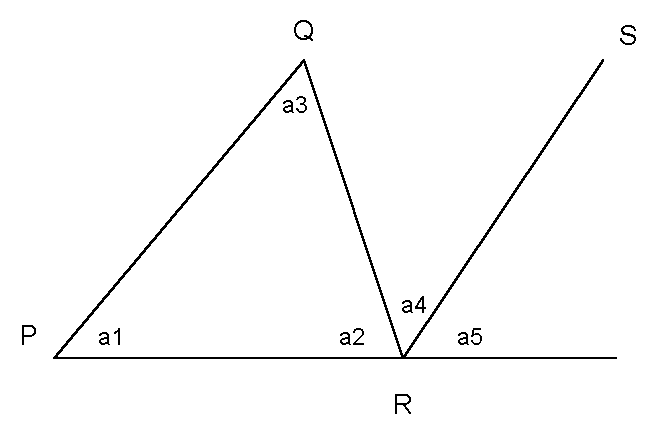
Our triangle is PQR. The angles in our triangle are a1, a2, and a3. Line RS is parallel to line PQ. This means that angle a5 is equal to angle a1 (see first picture above), and that angle a4 is equal to angle a3 (see second picture above). So, that means that a1+a2+a3 = a5+a2+a4 = a2+a4+a5. But a2+a4+a5 is equal to 180° (by definition)! So, this proves that the sum of angles in a triangle equals 180°, or QED as the mathematicians say.
| Gödel's Theorem |
Now it gets complicated. A guy named Kurt Gödel caused quite a bit of a stir in mathematics early last century, when he proved that there are mathematical statements that are either true or false, but that cannot be proven to be true or false. I'm paraphrasing a little bit here. It's kind of difficult to appreciate this, but maybe the following statement can illustrate it a little.
This statement cannot be proven.
Now, if the statement is false, then it follows that it can be proven, therefore it has to be true. If it is true, then it cannot be proven. It cannot be false, so it has to be true, so it cannot be proven! Funny, huh? All sorts of interesting philosophical conclusions have been drawn from this. I'm not going to comment on those...
Please send comments to webmaster@oldeloohuis.com.