Escape Velocity

Calculating Escape Velocity

First of all, what is escape velocity anyway? Escape velocity is the velocity that an object must have to escape the gravitational field of a body like the earth, or another planet, or any mass. That's my definition, by the way.

Why would you be interested, anyway? Well, you need to know this if you want to calculate how to fly to the moon, for example. Or maybe it would be interesting for other things as well...

So, let's assume we can neglect air resistance, and let's assume we are directing our object vertically, i.e. "straight up". What is the speed the object needs to have to escape from the 'gravity well'?

There are two things going on here. First, our object has a certain velocity upwards, away from the planet. Note that the object is not being propelled. Second, the gravity field of the planet is pulling our object down. Which of the two will win?

The first reaction is to think that the object will always come down eventually, since the planet keeps on pulling on it, and the object is not propelled. So, eventually, gravity will win, right?

Wrong. The thing I didn't mention yet, is that the higher our object is, the less gravity will be. Gravity diminishes with the square of the distance to the center of the planet. This is a consequence of Newton's Law of Gravity. We need more equations here, so let's see.

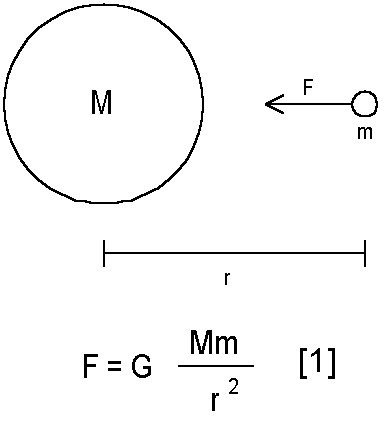
In English: two bodies with masses M and m will attract each other with a force that is proportional to the masses of the bodies, and inversely proportional to the square of the distance between the centers of the bodies. There is a constant in there as well.

F is the attracting (gravitational) force.
M is de mass of the first body,
m is the mass of the second body,
r is the distance between the centers,
G is the gravitational constant.

We have another equation that describes the motion of an object.

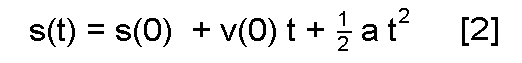
This describes the position of an object at a certain time t, given a start position (s(0)), a start velocity (v(0), in our case the escape velocity) and an accelleration a (in our case, the acceleration - or deceleration - caused by gravitation).

One more equation, Newton's Second Law of Motion (see text box later on, though)


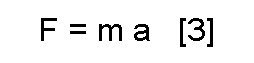
Combining [1] and [3] (they are equal) we find that:

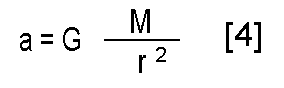
So, we could substitute [4] in [2] and try to find a solution (we need to fiddle with signs, since the direction of v(0) is opposite to that of a). However, this becomes quite complex, since there are dependencies between the value of s(t) and a. Maybe it is solvable (at the very least you can feed the problem to a computer and approximate the solution numerically), but it becomes too complex for me, I'm afraid.

Fortunately, there is a better way. We can calculate the potential energy of the object in the gravitational field. Some very basic physics state that:

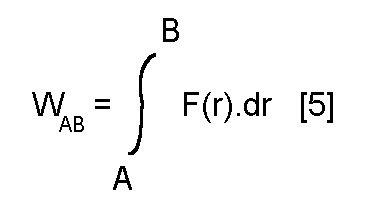
Where WAB is the amount of work (energy) required when moving an object with force F(r) over a distance dr, from point A to point B. Turns out that using [1] for the expression of force yields an integral that can be solved easily.

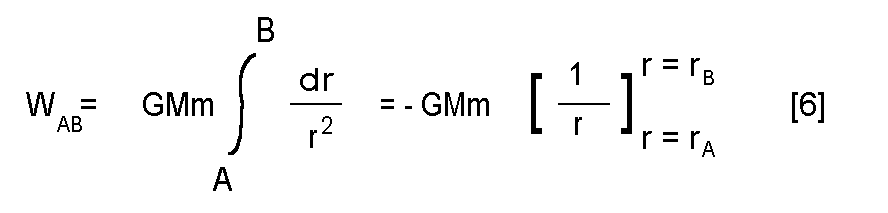
Now, if we choose our point B to be infinitely far away (no gravity there), and our point A to be on the surface of our planet, introduce U for the potential energy, we find that

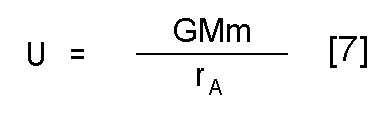
So, to escape the gravity of our planet, our object must have a kinetic energy that is equal to this potential energy. Since we know that the kinetic energy E of an object with mass m and velocity v is gven by

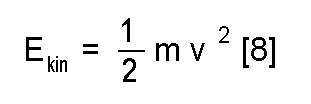
we find that

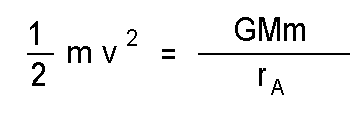
or

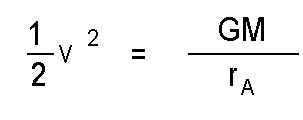
so

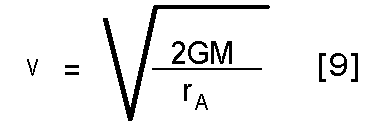
That's it. We're done. Just for fun, let's fill in some values and do a sanity check.

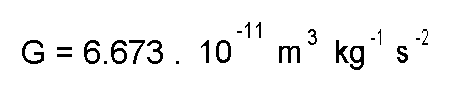
For Earth, we have

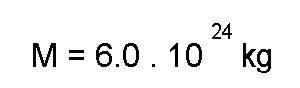
and

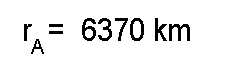
so,

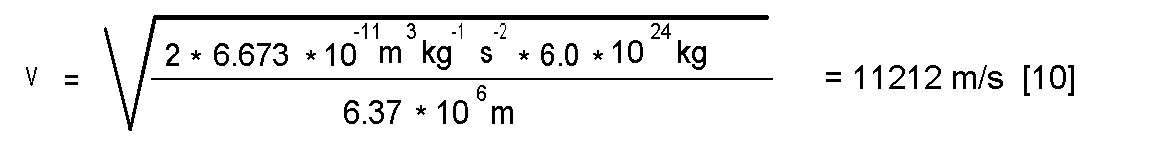
which agrees nicely with the known value. Just for kicks, let's do the same thing for Mars. Here we know that rm = 3397 km, and M = 6.4185 * 1023 kg, so we find that the escape velocity = 5.02 km/s, which also agrees nicely with literature.

I'm always somewhat confused by Newton's Second Law of Motion. You usually find it stated (as I did here) as:

F = m a,
where:

F is the force (in Newtons) applied to an object,
m is the mass (in kilograms) of the object,
and a is the acceleration (in m/(s^2)) of the object as a result of the applied force.

I always thought that the correct way to write it was:

F = dp/dt,

where p = m v (p is the momentum of the object),

with m the mass of the object,
and v de velocity of the object.

So, using the normal mathematical rules of differentiation, we find that:

F = dp/dt = d(mv)/dt = m dv/dt + v dm/dt = m a + v dm/dt

Note that a = dv/dt.

The term dm/dt indicates the change of mass per time unit, and this is usually 0, so we find:

F = m a

However, in the case of spaceships and rockets and all that, dm/dt is typically not 0 (a rocket loses much of its mass in the form of burnt fuel), so we can't just use F = m * a. Oh well.

Please send comments to webmaster@oldeloohuis.com.