| Accelerated Elevator |
We're getting into the theory of relativity here, and something that must be painfully obvious. It wasn't to me though.
Ok. A bit of history (I'm not responsible for inaccuracies...). When Albert Einstein had developed his special theory of relativity, which dealt with uniform (i.e. non-accelerated) motion, he tackled the problem of non-uniform (i.e. accelerated) motion. The result of this effort was the general theory of relativity. I'm not going to go into this too deeply, mostly because I don't really understand it all.
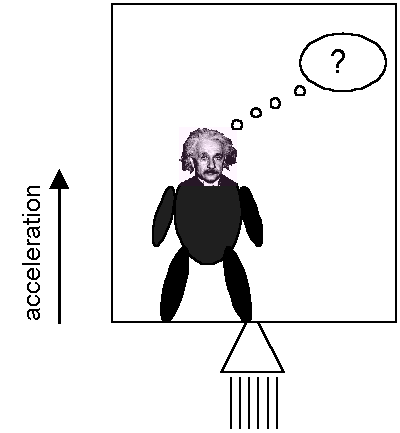
Anyway, to solve some problems regarding light rays being bent in certain situations, he stated his so-called Equivalence Principle. Let's look at the following picture (I have great artistic talents, don't you think?).

Hmm, this guy reminds me of someone...
Consider an elevator (Einstein refers to a chest) with an observer inside. The elevator is accelerated by a rocket (that was clear from the picture, right?). Due to the acceleration, the observer feels a force pressing him downward. According to the Equivalence Principle, the observer has every right to state that the elevator is not accelerated, but is subject to a gravitational field, like in the following picture.
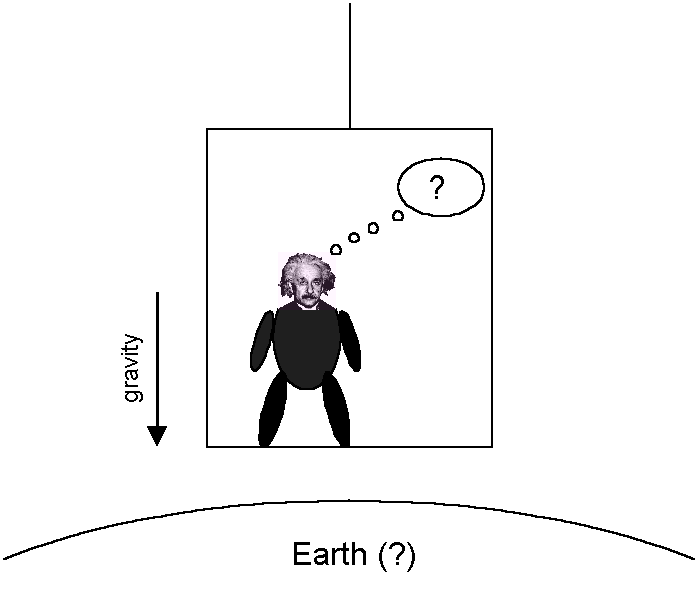
There's the same dude again. This elevator is hanging by a rope, by the way, it is not falling. So, according to Einstein, there is no physical experiment the observer can perform to determine if he is in an accelerated elevator, or in a stationary elevator in a gravitational field. No, there is no peeking out the window, the elevator has no windows. No cheating. Should have mentioned that earlier, I guess.
Now, when you read descriptions of this principle in physics textbooks or on the Web, you will almost always find something like "the observer in the accelerated elevator experiences a gravitational field as if it was caused by a planet or a star". Or words to that extent (in defense of Mr. Einstein, he specifically avoids wording like that, in his book Relativity he just talks about "a gravitational field").
Whoa! "as if it was caused by a planet or star"??? These things have a tendency to be spherical (more or less). Ignoring relativistic effects for the moment, that means that the gravitational filed of a planet like Earth has a dependency on the distance between the observer and the center of the Earth. The gravitational field in the accelerated elevator should be uniform.
| Taking the relativistic effects into account: the fact that the gravitational field inside the elevator is uniform is not entirely correct. Derivations (that I don't fully understand yet) in textbooks about general relativity show a non-uniformity of the gravitational field in the z-direction (or "up"). However, the field is uniform in the x-direction and y-direction (or "sideways"). The gravitational field of the earth will not be uniform in the x- and y-directions (the floor of the elevator is perfectly flat), if ever so slightly different from a uniform field. |
Now, it is true that in this case, for all practical means and purposes the field will be very close to uniform. Assuming the radius of the earth to be 6000 km, and our elevator to be 3 meters high (numbers are just for convenience), the ratio of the strength of the gravitational force between the top and the bottom of the elevator will be rougly (1/(6,000,003)2)/((1/6,000,000)2) = 0.999999 (take my word for it). So the difference is about 0.00001%.
However, we can replace earth with some other object that is much smaller. If we choose an object that has only a radius of 6 km, then we can choose its mass to be 1 millionth of the earth. This would give the same gravitational force on the surface as on earth. The mass density of this object would be 1000 times that of earth, so this would be a white dwarf or a neutron star or something, but that's not the point. Anyway, if we calculate the difference in gravitation between the top and bottom of the elevator again, we find a ratio of ((1/6003)^2)/((1/6000)^2) = 0.999. So, a difference of 0.1%. Still not very dramatic, but quite different from the first case.
The final point is that we need a mass that can generate a uniform field to have true equivalence. A spherical mass doesn't cut it, you need something that is perfectly flat and has infinite size in the x- and y-directions. I scribbled down a derivation of this somewhere, I'll put it here someday if I can be bothered to pound in the equations.
Conclusion is that (again) the thing that I missed (the field must be uniform) is apparently very obvious. The statement that a planet or star could generate an equivalent field to that in the elevator must be plain wrong, in my humble opinion.
Please send comments to webmaster@oldeloohuis.com.